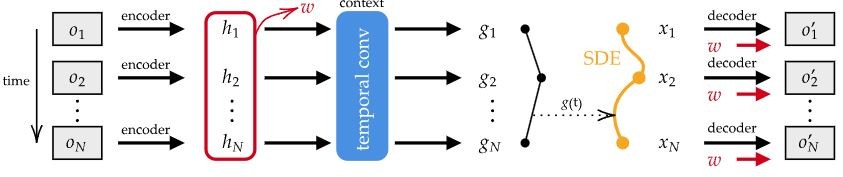
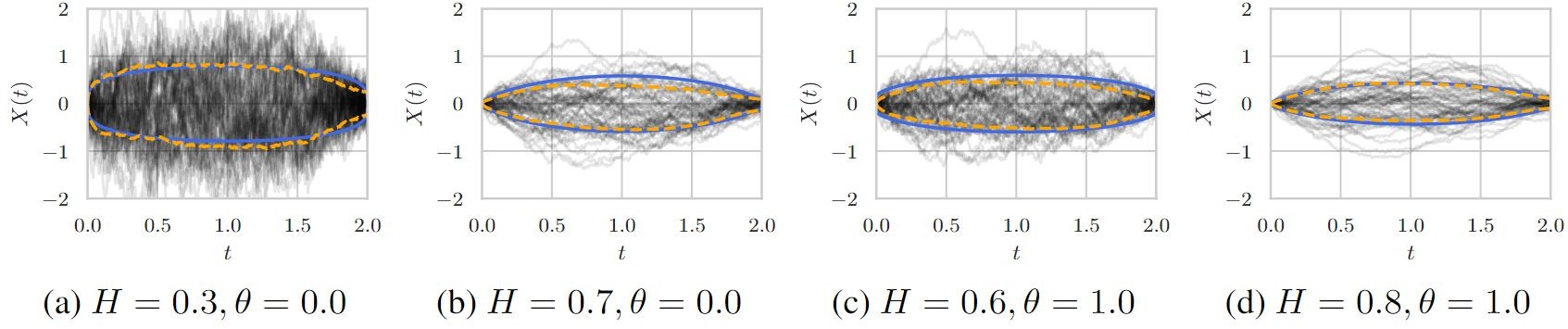
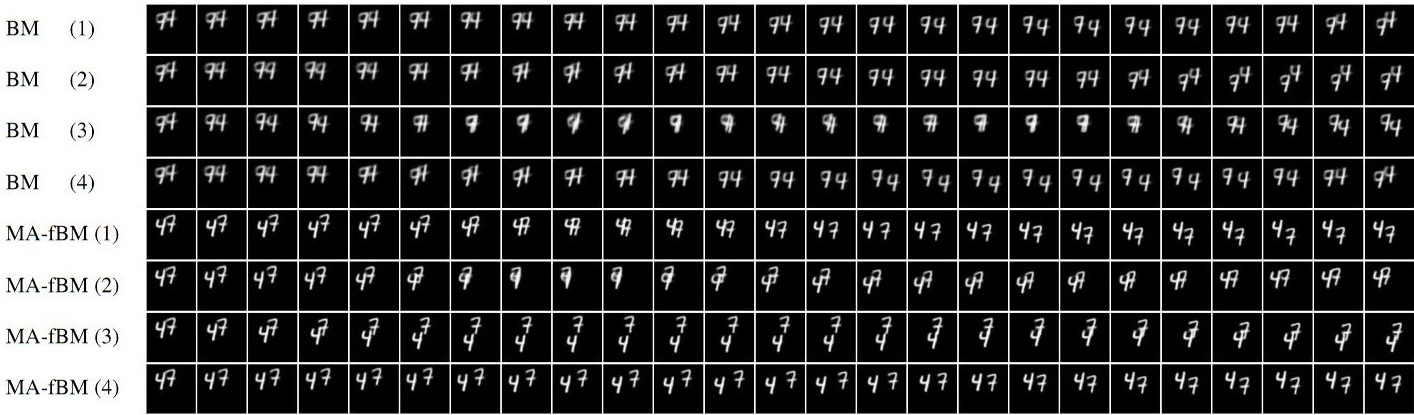
We present a novel variational framework for performing inference in (neural) stochastic differential equations (SDEs) driven by Markov-approximate fractional Brownian motion (fBM). SDEs offer a versatile tool for modeling real-world continuous-time dynamic systems with inherent noise and randomness. Combining SDEs with the powerful inference capabilities of variational methods, enables the learning of representative function distributions through stochastic gradient descent. However, conventional SDEs typically assume the underlying noise to follow a Brownian motion (BM), which hinders their ability to capture long-term dependencies. In contrast, fractional Brownian motion (fBM) extends BM to encompass non-Markovian dynamics, but existing methods for inferring fBM parameters are either computationally demanding or statistically inefficient.
In this paper, building upon the Markov approximation of fBM, we derive the evidence lower bound essential for efficient variational inference of posterior path measures, drawing from the well-established field of stochastic analysis. Additionally, we provide a closed-form expression to determine optimal approximation coefficients. Furthermore, we propose the use of neural networks to learn the drift, diffusion and control terms within our variational posterior, leading to the variational training of neural-SDEs. In this framework, we also optimize the Hurst index, governing the nature of our fractional noise. Beyond validation on synthetic data, we contribute a novel architecture for variational latent video prediction,—an approach that, to the best of our knowledge, enables the first variational neural-SDE application to video perception.